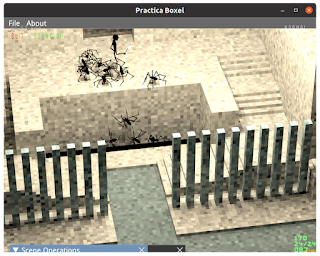
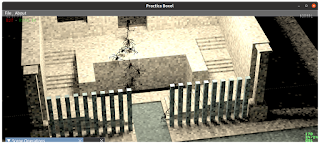
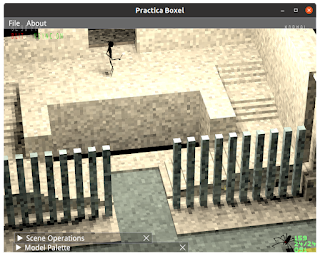
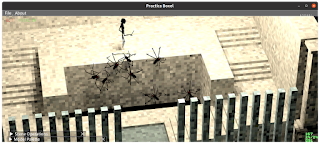
Computer monitors come in different aspect ratios. From the old school 4:3 to the ridiculous 32:9.
In my 3D games, I have to choose a Field-Of-View for the camera. Wide angle, or narrow angle views? To do this, the convention is to set a fixed vertical field of view, and then adopt the horizontal field of view that falls out of it, based on the image aspect ratio. I use this for all my 3D games: set the vertical F.o.V.
Fixing the Vertical Field of View, means that users on 4:3 monitors see less of the world, and users on ultra wide screen see more of the world. This could pose an unfair advantage.
An additional problem is that ultra wide aspect ratios lead to ultra wide angle views, which lead to a lot of distorted shapes in the corners of the screen.
But fixing the Horizontal Field of View instead, would mean that users on wide-screen would see less of the world (at top and bottom parts of screen.) This made me wonder... what if I were to fix the angle for the diagonal field instead? Fixed for all users. And then let the Horizontal/Vertical angles fall out of this.
Definitely worth an experiment! So let's do some trigonometry!
Problem: given a fixed angle for the diagonal field of view... what are the corresponding Vertical and Horizontal fields of view?
Given the fixed diagonal field of view angle α, and a given image height h, and image diagonal d, we need merely two equations to derive the vertical field of view angle β.
And with that angle β we can set up our projection matrix the usual way.
When we do all this, we go from extremist views (with fixed vertical FoV) like these:
...to more moderate views (with fixed diagonal FoV) like the ones below. Note that the view angles change less than in the case above, between aspect ratios. The narrow aspect ratio does not show that much less on left/right, and for what it loses on the sides, it wins a little on top/bottom. I think this approach is a keeper!
For completeness, the code, which is trivial:
float vertical_fov_from_diagonal_fov( float a, float w, float h )
{
const float d = sqrtf(w*w + h*h);
const float m = d / ( 2 * tanf( a / 2 ) );
const float b = 2 * atanf( h / (2*m) );
return b;
}